Maximum Common Divisor (GCD): What It Is, How to Calculate It and Examples (24 and 36)
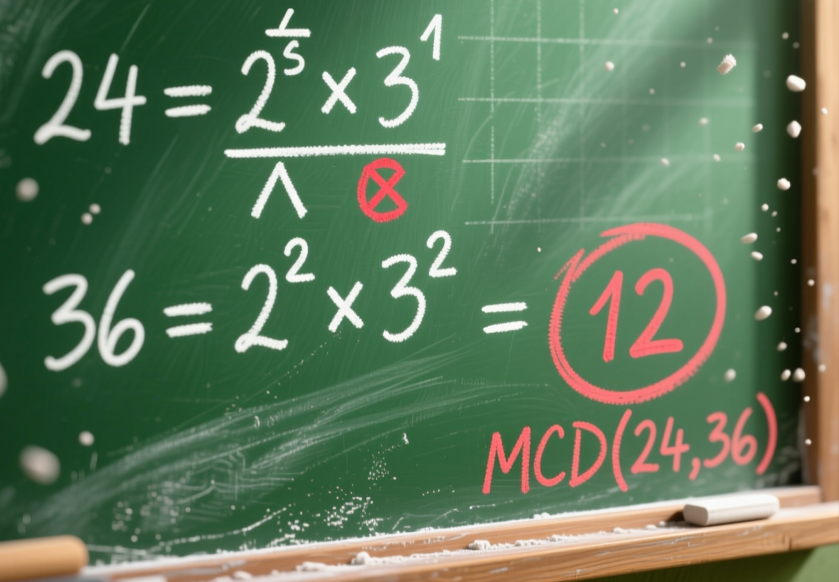
Visual representation of GCD calculation methods
Have you ever wondered how your online purchases are protected? The answer might surprise you: it’s related to mathematics, specifically to the Greatest Common Divisor (GCD). In this complete guide, we explain what GCD is, how to calculate it with practical examples like 24 and 36, and you’ll discover its crucial application in information security.
What is the Greatest Common Divisor (GCD)?
The Greatest Common Divisor (GCD) of two or more numbers is the largest number that divides each of them exactly without leaving a remainder. It’s a fundamental concept in arithmetic that has applications ranging from basic mathematical problems to modern cryptography.
For example, the GCD of 8 and 12 is 4, because 4 is the largest number that divides both 8 (8÷4=2) and 12 (12÷4=3).
How to Calculate the GCD? Practical Methods
Method 1: Prime Factorization
This method consists of decomposing the numbers into their prime factors and taking the common factors raised to the smallest exponent.
Example: Calculate the GCD of 24 and 36
- 24 = 2³ × 3¹
- 36 = 2² × 3²
Common factors: 2 and 3. We take the smallest exponents: 2² and 3¹.
GCD(24, 36) = 2² × 3¹ = 4 × 3 = 12
Method 2: Euclidean Algorithm
This method, more efficient for large numbers, is based on successive divisions:
- Divide the larger number by the smaller one
- Then, divide the divisor by the remainder obtained
- Repeat until the remainder is 0
- The last divisor (different from zero) is the GCD
Example: GCD of 24 and 36 with Euclid
- 36 ÷ 24 = 1 (remainder 12)
- 24 ÷ 12 = 2 (remainder 0)
GCD(24, 36) = 12
Practical Examples of GCD
- GCD of 6 and 8: Factors: 6=2×3, 8=2³. Common factor: 2¹. GCD=2
- GCD of 18 and 27: 18=2×3², 27=3³. Common factor: 3². GCD=9
- GCD of 12, 18 and 24: 12=2²×3, 18=2×3², 24=2³×3. Common factors: 2¹×3¹. GCD=6
Applications of GCD in Real Life
In Everyday Mathematics:
- Simplifying fractions: GCD is used to reduce fractions to their simplest form.
- Distribution problems: Dividing materials into equal parts without leftovers.
- Calculating repetitive patterns: Finding how often simultaneous events repeat.
Advanced Application: GCD in Cryptography
In real life, the Greatest Common Divisor (GCD) is fundamental for the security of your data. A practical and crucial application is in the cryptography that protects your online purchases.
Encryption algorithms, like RSA, depend on the difficulty of factoring large numbers. Here, GCD is an essential tool in advanced factorization methods, such as Pollard’s «rho» algorithm, which tries to find factors of a number by calculating the GCD between the number and certain generated values.
If the GCD (a non-trivial factor) were found, the cryptographic key would be broken. Thus, the security of your online banking transactions resides, in part, in the computational difficulty of calculating the GCD of astronomically large numbers.
Relationship Between GCD and Least Common Multiple (LCM)
It’s important not to confuse GCD with LCM (Least Common Multiple). While GCD looks for the greatest common divisor, LCM finds the smallest common multiple. There is a mathematical relationship between them:
For two numbers a and b: GCD(a,b) × LCM(a,b) = a × b
Conclusion
The Greatest Common Divisor is much more than an abstract mathematical concept. From simplifying fractions to protecting the security of our online transactions, GCD demonstrates that basic mathematics has profound applications in our technological world.
Now that you understand what GCD is, how to calculate it with methods like the Euclidean algorithm, and have seen practical examples like the GCD of 24 and 36, you can appreciate its true utility that goes far beyond the classroom.
Ready to put what you’ve learned into practice? Calculate the GCD of some numbers on your own and discover why this concept remains relevant after thousands of years!