Máximo Común Divisor (MCD): Qué es, Cómo Calcularlo y Ejemplos (24 y 36)
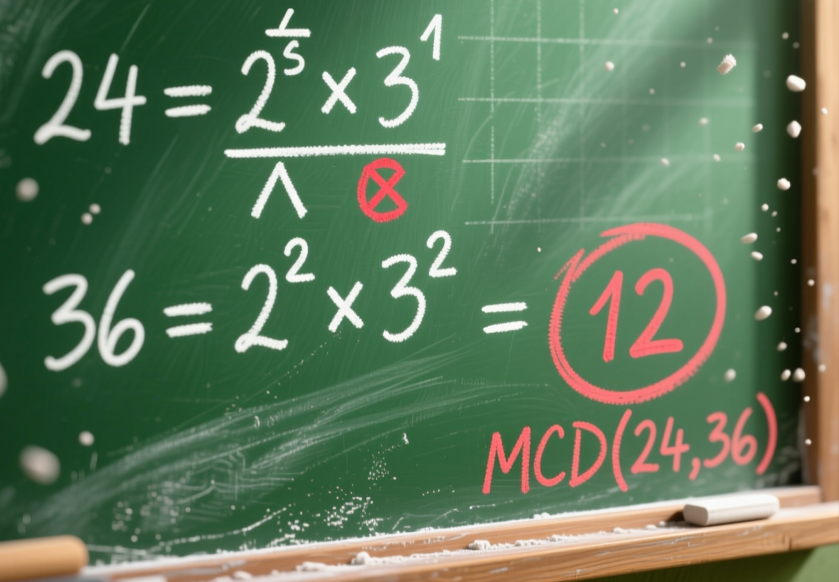
¿Alguna vez te has preguntado cómo se protegen tus compras online? La respuesta podría sorprenderte: está relacionada con las matemáticas, específicamente con el Máximo Común Divisor (MCD). En esta guía completa, te explicamos qué es el MCD, cómo calcularlo con ejemplos prácticos como el de 24 y 36, y descubrirás su crucial aplicación en la seguridad informática.
¿Qué es el Máximo Común Divisor (MCD)?
El Máximo Común Divisor (MCD) de dos o más números es el mayor número que divide exactamente a cada uno de ellos sin dejar resto. Es un concepto fundamental en aritmética que tiene aplicaciones que van desde problemas matemáticos básicos hasta la criptografía moderna.
Por ejemplo, el MCD de 8 y 12 es 4, porque 4 es el número más grande que divide tanto a 8 (8÷4=2) como a 12 (12÷4=3).
¿Cómo calcular el MCD? Métodos prácticos
Método 1: Descomposición en factores primos
Este método consiste en descomponer los números en sus factores primos y tomar los factores comunes elevados al menor exponente.
Ejemplo: Calcular el MCD de 24 y 36
- 24 = 2³ × 3¹
- 36 = 2² × 3²
Factores comunes: 2 y 3. Tomamos los menores exponentes: 2² y 3¹.
MCD(24, 36) = 2² × 3¹ = 4 × 3 = 12
Método 2: Algoritmo de Euclides
Este método, más eficiente para números grandes, se basa en divisiones sucesivas:
- Divide el número mayor entre el menor
- Luego, divide el divisor entre el residuo obtenido
- Repite hasta que el residuo sea 0
- El último divisor (distinto de cero) es el MCD
Ejemplo: MCD de 24 y 36 con Euclides
- 36 ÷ 24 = 1 (residuo 12)
- 24 ÷ 12 = 2 (residuo 0)
MCD(24, 36) = 12
Ejemplos prácticos de MCD
- MCD de 6 y 8: Factores: 6=2×3, 8=2³. Factor común: 2¹. MCD=2
- MCD de 18 y 27: 18=2×3², 27=3³. Factor común: 3². MCD=9
- MCD de 12, 18 y 24: 12=2²×3, 18=2×3², 24=2³×3. Factores comunes: 2¹×3¹. MCD=6
Aplicaciones del MCD en la vida real
En matemáticas cotidianas:
- Simplificación de fracciones: El MCD se usa para reducir fracciones a su mínima expresión.
- Problemas de repartición: Dividir materiales en partes iguales sin que sobre nada.
- Cálculo de patrones repetitivos: Encontrar cada cuánto se repiten eventos simultáneos.
Aplicación avanzada: El MCD en criptografía
En la vida real, el Máximo Común Divisor (MCD) es fundamental para la seguridad de tus datos. Una aplicación práctica y crucial está en la criptografía que protege tus compras por internet.
Algoritmos de cifrado, como RSA, dependen de la dificultad de factorizar números grandes. Aquí, el MCD es una herramienta esencial en métodos de factorización avanzados, como el algoritmo «rho» de Pollard, que intenta encontrar factores de un número calculando el MCD entre el número y ciertos valores generados.
Si se encontrara el MCD (un factor no trivial), se rompería la clave criptográfica. Así, la seguridad de tus transacciones bancarias en línea reside, en parte, en la dificultad computacional de calcular el MCD de números astronómicamente grandes.
Relación entre MCD y Mínimo Común Múltiplo (MCM)
Es importante no confundir el MCD con el MCM (Mínimo Común Múltiplo). Mientras el MCD busca el mayor divisor común, el MCM encuentra el menor múltiplo común. Existe una relación matemática entre ambos:
Para dos números a y b: MCD(a,b) × MCM(a,b) = a × b
Conclusión
El Máximo Común Divisor es mucho más que un concepto matemático abstracto. Desde simplificar fracciones hasta proteger la seguridad de nuestras transacciones online, el MCD demuestra que las matemáticas básicas tienen aplicaciones profundas en nuestro mundo tecnológico.
Ahora que comprendes qué es el MCD, cómo calcularlo con métodos como el algoritmo de Euclides, y has visto ejemplos prácticos como el MCD de 24 y 36, puedes apreciar su verdadera utilidad que va mucho más allá del aula.
¿Listo para poner en práctica lo aprendido? ¡Calcula el MCD de algunos números por tu cuenta y descubre por qué este concepto sigue siendo relevante después de miles de años!