Lucas lehmer test for beginners 😎 😛

Lucas Lehmer Test: What it is, How it Works, and its Application in Prime Numbers

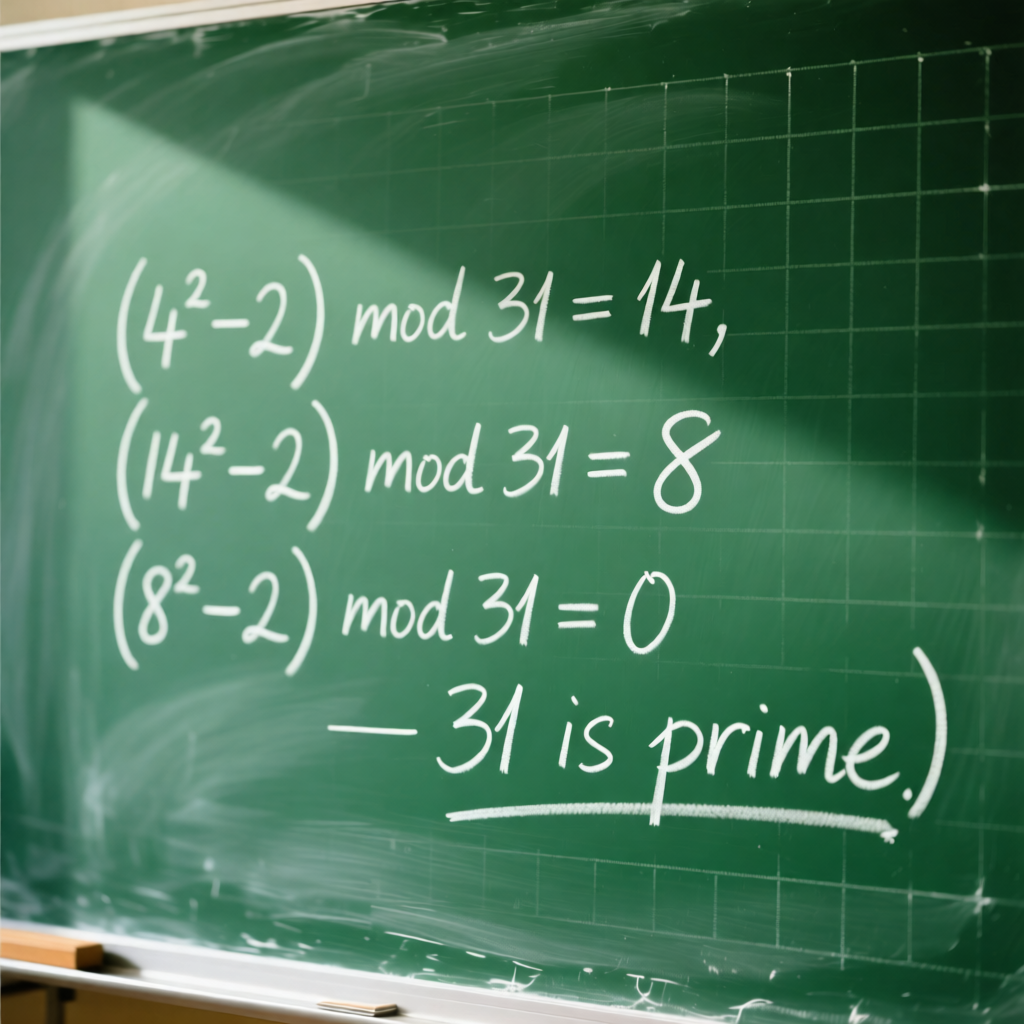
Did you know that the largest known prime numbers were discovered using a centuries-old mathematical test? The Lucas-Lehmer test is a specialized algorithm that revolutionized the search for giant prime numbers. In this comprehensive guide, we will explore how this test works, its practical application, and why it remains relevant in the era of modern computing.

What is the Lucas Lehmer Test?

The Lucas Lehmer test is a deterministic algorithm designed specifically to verify whether a Mersenne number (numbers of the form 2^p – 1, where p is prime) is prime. Originally developed by Édouard Lucas in 1878 and refined by Derrick Lehmer in 1930, this test is extraordinarily efficient compared to general primality testing methods.

Mersenne Numbers: These are numbers that follow the formula M_p = 2^p – 1, where p is a prime number. Not all Mersenne numbers are prime, but all Mersenne primes follow this form.

How Does the Lucas Lehmer Test Work?

The Algorithm Step by Step

The Lucas Lehmer test follows a specific sequence to determine if M_p = 2^p – 1 is prime:

Define the sequence: S₀ = 4
For k from 1 to p-2, calculate: S_k = (S_k-1² – 2) mod M_p
If S_p-2 ≡ 0 (mod M_p), then M_p is prime
Otherwise, M_p is composite

S₀ = 4
Sₖ = (Sₖ₋₁² – 2) mod Mₚ
If Sₚ₋₂ ≡ 0 mod Mₚ → Mₚ is prime

Practical Example: Testing M₃ (2³ – 1 = 7)

Step 1: M₃ = 2³ – 1 = 7

Step 2: S₀ = 4

Step 3: S₁ = (4² – 2) mod 7 = (16 – 2) mod 7 = 14 mod 7 = 0

Step 4: Since S₁ = 0 and p-2 = 1, then M₃ = 7 is prime

Example: Testing M₅ (2⁵ – 1 = 31)

Step 1: M₅ = 2⁵ – 1 = 31

Step 2: S₀ = 4

Step 3: S₁ = (4² – 2) mod 31 = 14

Step 4: S₂ = (14² – 2) mod 31 = 194 mod 31 = 8

Step 5: S₃ = (8² – 2) mod 31 = 62 mod 31 = 0

Step 6: Since S₃ = 0 and p-2 = 3, then M₅ = 31 is prime

Real-World Applications

Search for Large Prime Numbers

GIMPS Project: The Great Internet Mersenne Prime Search uses this test to search for new record-breaking prime numbers
Fast verification: Allows verification of extremely large numbers with computational efficiency
World records: All the largest known prime numbers were verified with this test

Application in Cryptography

The Lucas Lehmer test has crucial implications in modern cryptography. Although not used directly in cryptographic algorithms, the search for large prime numbers is fundamental for systems like RSA.

Mersenne primes, verified through this test, provide important case studies for understanding the properties of prime numbers. This understanding helps improve prime number generation algorithms used in:

Cryptographic key generation
SSL/TLS security protocols
Digital signature systems
Elliptic curve cryptography

The efficiency of the Lucas Lehmer test allows verifying numbers with millions of digits, which would be computationally prohibitive with general primality testing methods.

Limitations and Considerations

Important: The Lucas Lehmer test only works for Mersenne numbers. For other numbers, different primality tests such as the Miller-Rabin test or the AKS test must be used.

Specific to Mersenne: Only applies to numbers of the form 2^p – 1
Computational complexity: O(p³) operations for large numbers
Storage: Requires handling extremely large numbers during calculation

History and Curiosities

1878: Édouard Lucas proves that M₁₂₇ is prime (this record stood for 75 years)
1930: Derrick Lehmer formalizes and improves the algorithm
1996: GIMPS Project discovers M₁₃₄₆₆₉₁₇ using this test
2018: M₈₂₅₈₉₉₃₃ is discovered, a number with 24,862,048 digits

Computational Implementation

Algorithm pseudocode:

function lucas_lehmer_test(p):
    if p is not prime: return COMPOSITE
    M_p = 2^p - 1
    s = 4
    for i from 1 to p-2:
        s = (s^2 - 2) mod M_p
    if s == 0:
        return PRIME
    else:
        return COMPOSITE

Conclusion

The Lucas Lehmer test represents one of the algorithmic jewels of number theory. Its elegant mathematical simplicity contrasts with its extraordinary practical power, allowing the verification of numbers with millions of digits that would be unreachable using conventional methods.

From its original formulation in the 19th century to its implementation in modern distributed computing projects, this test continues to expand the frontiers of mathematical knowledge. Its role in the discovery of record-breaking prime numbers and its indirect implications in cryptography demonstrate how pure mathematics finds surprising applications in the contemporary technological world.

Are you interested in participating in this mathematical quest? The GIMPS project allows anyone to contribute computing power to search for the next Mersenne prime, continuing a mathematical tradition that connects 19th-century genius with 21st-century technology.