Test de Lucas Lehmer: Qué es, Cómo Funciona y su Aplicación en Números Primos
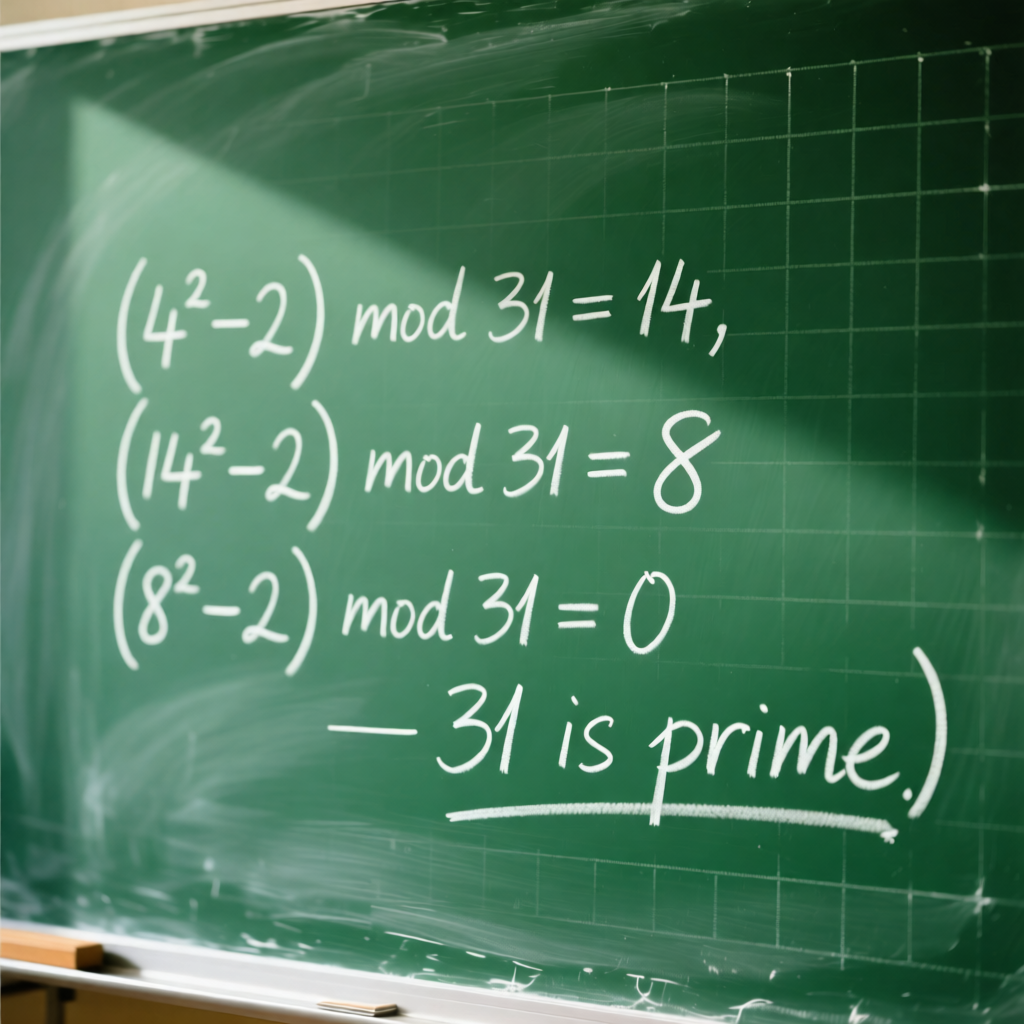
¿Sabías que los números primos más grandes conocidos fueron descubiertos usando una prueba matemática centenaria? El test de Lucas-Lehmer es un algoritmo especializado que revolucionó la búsqueda de números primos gigantes. En esta guía completa, exploraremos cómo funciona este test, su aplicación práctica y por qué sigue siendo relevante en la era de la computación moderna.
¿Qué es el Test de Lucas Lehmer?
El test de Lucas Lehmer es un algoritmo determinista diseñado específicamente para verificar si un número de Mersenne (números de la forma 2p – 1, donde p es primo) es primo. Desarrollado originalmente por Édouard Lucas en 1878 y refinado por Derrick Lehmer en 1930, este test es extraordinariamente eficiente comparado con métodos generales de prueba de primalidad.
Números de Mersenne: Son números que siguen la fórmula Mp = 2p – 1, donde p es un número primo. No todos los números de Mersenne son primos, pero todos los primos de Mersenne siguen esta forma.
¿Cómo Funciona el Test de Lucas Lehmer?
El Algoritmo Paso a Paso
El test de Lucas Lehmer sigue una secuencia específica para determinar si Mp = 2p – 1 es primo:
- Definir la secuencia: S0 = 4
- Para k desde 1 hasta p-2, calcular: Sk = (Sk-12 – 2) mod Mp
- Si Sp-2 ≡ 0 (mod Mp), entonces Mp es primo
- En caso contrario, Mp es compuesto
Sₖ = (Sₖ₋₁² – 2) mod Mₚ
Si Sₚ₋₂ ≡ 0 mod Mₚ → Mₚ es primo
Ejemplo Práctico: Probando M₃ (2³ – 1 = 7)
Paso 1: M₃ = 2³ – 1 = 7
Paso 2: S₀ = 4
Paso 3: S₁ = (4² – 2) mod 7 = (16 – 2) mod 7 = 14 mod 7 = 0
Paso 4: Como S₁ = 0 y p-2 = 1, entonces M₃ = 7 es primo
Ejemplo: Probando M₅ (2⁵ – 1 = 31)
Paso 1: M₅ = 2⁵ – 1 = 31
Paso 2: S₀ = 4
Paso 3: S₁ = (4² – 2) mod 31 = 14
Paso 4: S₂ = (14² – 2) mod 31 = 194 mod 31 = 8
Paso 5: S₃ = (8² – 2) mod 31 = 62 mod 31 = 0
Paso 6: Como S₃ = 0 y p-2 = 3, entonces M₅ = 31 es primo
Aplicaciones en el Mundo Real
Búsqueda de Números Primos Grandes
- Proyecto GIMPS: El Great Internet Mersenne Prime Search utiliza este test para buscar nuevos números primos récord
- Verificación rápida: Permite verificar números extremadamente grandes con eficiencia computacional
- Récords mundiales: Todos los números primos más grandes conocidos fueron verificados con este test
Aplicación en Criptografía
El test de Lucas Lehmer tiene implicaciones cruciales en criptografía moderna. Aunque no se usa directamente en algoritmos criptográficos, la búsqueda de números primos grandes es fundamental para sistemas como RSA.
Los números primos de Mersenne, verificados mediante este test, proporcionan casos de estudio importantes para entender las propiedades de los números primos. Esta comprensión ayuda a mejorar los algoritmos de generación de números primos utilizados en:
- Generación de claves criptográficas
- Protocolos de seguridad SSL/TLS
- Sistemas de firma digital
- Criptografía de curva elíptica
La eficiencia del test de Lucas Lehmer permite verificar números con millones de dígitos, lo que sería computacionalmente prohibitivo con métodos generales de prueba de primalidad.
Limitaciones y Consideraciones
Importante: El test de Lucas Lehmer solo funciona para números de Mersenne. Para otros números, se deben usar pruebas de primalidad diferentes como el test de Miller-Rabin o el test AKS.
- Específico para Mersenne: Solo aplica a números de la forma 2p – 1
- Complejidad computacional: O(p³) operaciones para números grandes
- Almacenamiento: Requiere manejar números extremadamente grandes durante el cálculo
Historia y Curiosidades
- 1878: Édouard Lucas demuestra que M₁₂₇ es primo (este récord se mantuvo por 75 años)
- 1930: Derrick Lehmer formaliza y mejora el algoritmo
- 1996: Proyecto GIMPS descubre M₁₃₄₆₆₉₁₇ usando este test
- 2018: Se descubre M₈₂₅₈₉₉₃₃, un número con 24,862,048 dígitos
Implementación Computacional
Pseudocódigo del algoritmo:
function lucas_lehmer_test(p):
if p no es primo: return COMPUESTO
M_p = 2^p - 1
s = 4
for i from 1 to p-2:
s = (s^2 - 2) mod M_p
if s == 0:
return PRIMO
else:
return COMPUESTO
Conclusión
El test de Lucas Lehmer representa una de las joyas algorítmicas de la teoría de números. Su elegante simplicidad matemática contrasta con su extraordinaria potencia práctica, permitiendo verificar números con millones de dígitos que serían inalcanzables mediante métodos convencionales.
Desde su formulación original en el siglo XIX hasta su implementación en proyectos de computación distribuida moderna, este test continúa expandiendo las fronteras del conocimiento matemático. Su papel en el descubrimiento de números primos récord y sus implicaciones indirectas en criptografía demuestran cómo las matemáticas puras encuentran aplicaciones sorprendentes en el mundo tecnológico contemporáneo.
¿Te interesa participar en esta búsqueda matemática? El proyecto GIMPS permite que cualquier persona contribuya con potencia computacional para buscar el próximo número primo de Mersenne, continuando una tradición matemática que conecta el genio del siglo XIX con la tecnología del siglo XXI.